Computational Physics

The graduate program in Computational Physics is being developed by Dr. Vladimir Florinski, a winner of the prestigious National Science Foundation CAREER award.

The Space Science Department with its close partnership with CSPAR and NASA's Marshall Space Flight Center has emerged as a regional leader in computational science research and education. Modern research in physics is inconceivable without a solid knowledge of computational methods. This program aims to prepare the future scientists for the realities and demands of modern computational environment. Students from a diverse range of backgrounds from science and engineering to business and finance, are encouraged to enroll. The curriculum is developed with input from the Huntsville area science and technology business community. We currently offer 4 courses within the program:

SPA 662 Computational Physics

This course provides a broad introduction to computational methods with applications to classical dynamics, electromagnetism, quantum mechanics, and statistical physics. It is taught using an actual programming language (C and C++) and teaches how to develop, compile, and run scientific codes. We learn numerical integration and differentiation, root finding, data fitting, numerical linear algebra, introductory Monte-Carlo method, linear and nonlinear ODEs, Fourier analysis, finite difference methods for elliptic, parabolic, and hyperbolic partial differential equations, and nonlinear wave propagation. Students also learn how to graph and visualize their results using open source visualization software. Every class we have an interactive session where students compete to finish a small computational project in real time. In place of a final exam students complete a class projects on applying computational methods to their own research field. Textbooks are Landau, Paez, and Bordeinau "Computational Physics" and Pang "An Introduction to Computational Physics". This course is offered every year.

Selected 2012 student research presentations

• Laxman Adhikari, "Turbulence transport model applied to space physics and astrophysics"
• Matthew Bedford, "A high resolution scheme for the MHD equations"
• Vandiver Chaplin, "Pulse-pileup: fitting a non-linear empirical model using Gauss-Newton algorithm and Simulation of a stochastic Poisson process"
• Junxiang Hu, "Power spectrum, cross helicity, and residual energy analysis of current sheets' effect on solar wind turbulence"
• Xiaocan Li, "1D particle-in-cell electromagnetic code"
• Scott Ripperda, "Retarded vector potentials and chaotic magnetic fields"
• Shirley Wu, "Pickup ion distributions"

Selected 2013 student research presentations

• Samer Alnussirat, "Sputtering of lunar regolith by solar wind protons and heavy ions"
• Preethi Manoharan, "Time-varying map of the global solar wind speed"
• Phyllis Whittlesey, "Particle trajectory in a Wien filter"

SPA 689 (Special Topics) Computational Plasma Physics

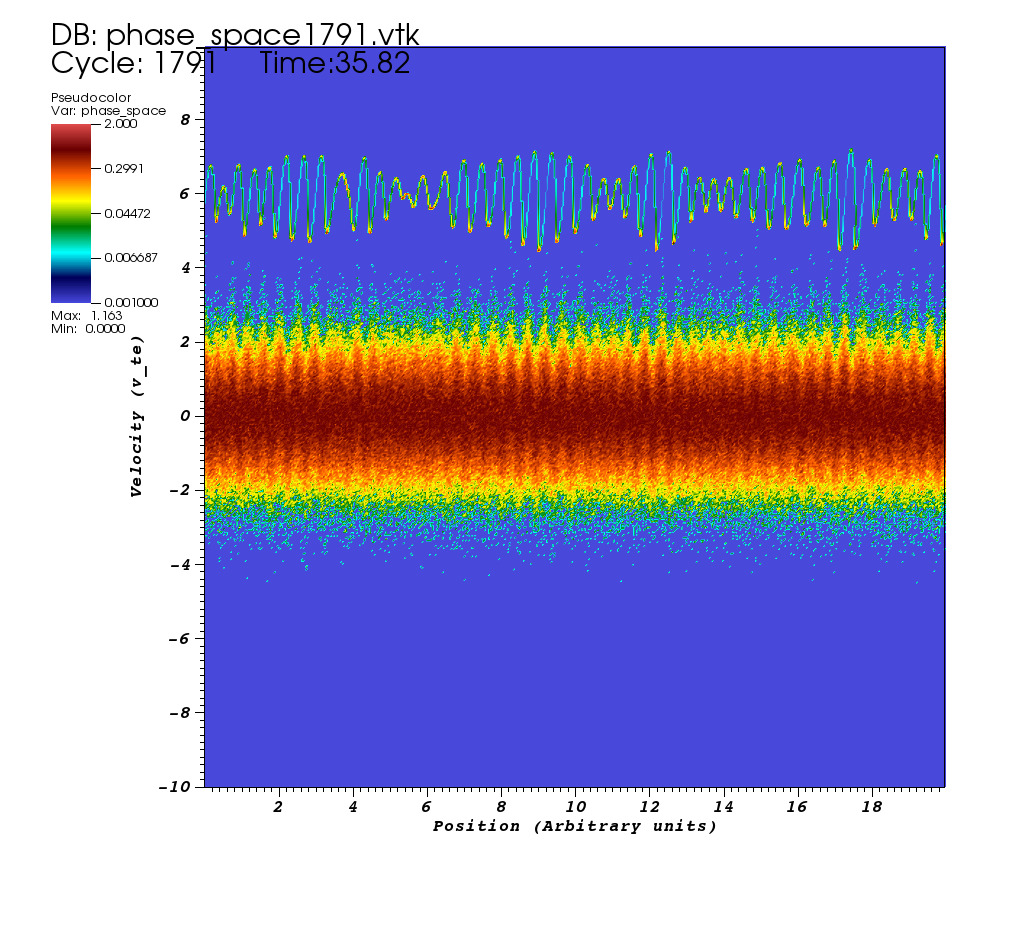Space and fusion plasma environments support a rich variety of physical phenomena, including plasma waves, instabilities, turbulence, and acceleration of charged particles. Computer simulations represent a powerful tool to model these processes, many of which cannot be readily reproduced in a lab. This course will introduce the two main classes of kinetic plasma simulations, particle-mesh and direct Vlasov, with the main emphasis on the particle methods. We will cover both full particle (PIC) and quasineutral (hybrid) models. Starting with gridless theory, we will proceed to particle trajectory integration methods (“particle push”), introduce different cloud representations for macro-particles, discuss Maxwell field solvers in electrostatic and magneto-inductive approximations, and eventually develop a complete solution sequence, including boundary conditions and loading of initial distributions. Most of the methods will be developed in one dimension; their extension to 2D and 3D will be outlined whenever possible, and spectral versions introduced for a few selected cases. We will also practice several common computational plasma problems, including a ring-beam instability, a collisionless shock wave, and (time permitting) magnetic reconnection. By the end of the course the students should be able to write, from scratch, their own kinetic plasma simulation code using the C programming language. Because of emphasis on hands on experience with plasma simulations, students are required to bring their laptop computer to class to practice code development and analyzing the simulation results. Recommended textbooks are Birdsall and Langdon "Plasma Physics via Computer Simulation", Tajima “Computational Plasma Physics”, and Lipatov “The Hybrid Multiscale Simulation Technology”.

SPA 663 Computational Fluid Dynamics and MHD

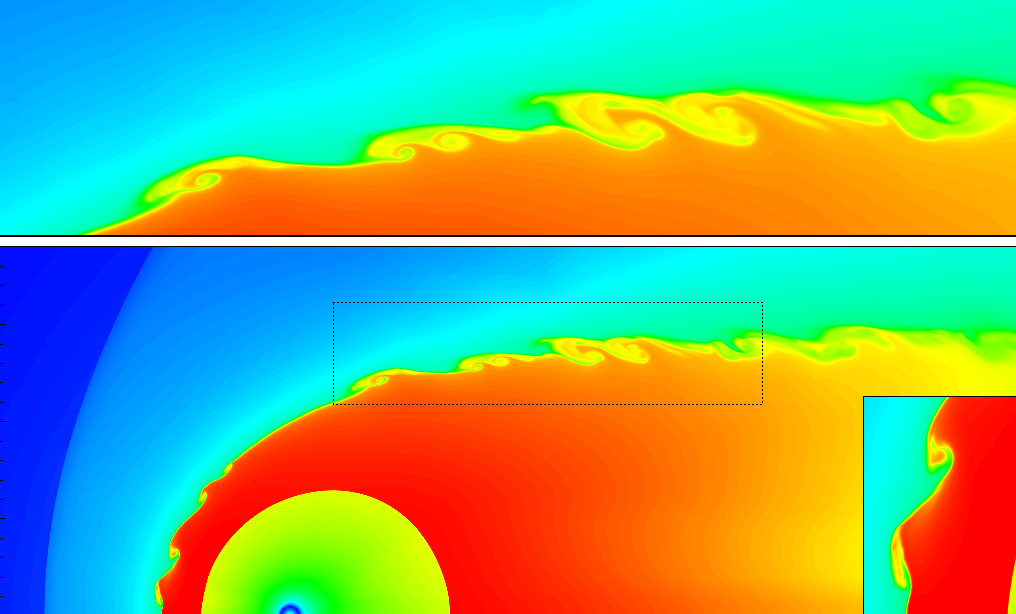The aim of the course is to give graduate students knowledge of the numerical approaches to solve gas dynamics and magnetohydrodynamics (MHD) equations sufficient for performing independent computations of plasma flows in laboratory and astrophysical environments. This is a computational fluid dynamics (CFD) and MHD course which describes not only numerical schemes, but also mathematically justified ways to formulate physical problems and appropriate boundary conditions. The course starts with a brief description of finite-difference and finite-volume approximations for the advection equations, accompanied by their stability and accuracy analysis. We consider traditional (central and upwind) Lax-Friedrichs, Lax-Wendroff, Beam-Warming, MacCormack, and Courant-Isaacson-Rees schemes, and their total variation diminishing analogues. The flux corrected transport (FCT) approach is used to introduce the notion of contemporary nonlinear schemes. All of these schemes are used throughout the course to solve CFD and MHD problems of different complexity as homework and projects. Different approaches to solve gas dynamics and MHD Riemann problems are discussed together with their application to systems of PDEs. Particular attention is paid to discontinuous solutions obtained with shock-capturing and shock-fitting methods. The evolutionary diagram for the MHD system is considered, and examples of spurious, nonevolutionary solutions are given as well as approaches to avoid them in numerical simulations. Numerical approaches to magnetic field divergence cleaning are analyzed and compared. Textbooks are Kulikovski, Pogorelov, and Semenov "Mathematical Aspects of Numerical Solutions of Hyperbolic Systems" and LeVeque "Finite Difference Methods for Ordinary and Partial Differential Equations".

SPA 689 (Special Topics) Stochastic Methods in Computational Physics

This course will provide an introduction to stochastic processes, Ito calculus and stochastic differential equations (SDEs). Emphasis will be on the differential Chapman-Kolmogorov equation and its special cases such as diffusion, Levi flights, and jump processes. We will discuss numerical solution methods for SDEs including Euler-Maruyama, Milstein, and Runge-Kutta explicit and implicit schemes. Applications will include turbulent diffusion, dynamical system stability, and some examples from chemistry, biology, and finance. A background in undergraduate probability theory and programming (C/C++) is highly recommended. Students are required to bring their laptop computer for in class exercises. Recommended textbooks are Gardiner, "Stochastic Methods" and Kloeden and Platen, "Numerical Solutions of Stochastic Differential Equations".

SPA 689 (Special Topics) Supercomputer Lab for Physical Sciences

This course will use a hands-on approach to introduce graduate students with a background in physical or natural sciences to modern HPC technologies. It will cover three common parallelization frameworks (MPI, pthreads, CUDA) applied to problems in gas dynamics, transport, and plasma physics.

Upon completion of this course, the student will be able to:

• Perform research level numerical simulations of three different classes of physics problems using a representative cross-section of modern day high performance computing technology,
• Efficiently use three classes of parallelization frameworks, the distributed memory message passing model, the shared memory threads model, and the single program/multiple data graphic processor model.
• Write scientific codes based on MPI, pthreads, and Nvidia CUDA C and C++ interfaces.