Modeling, Simulation and Analysis
Projects
The goals of this project are to improve operational flood forecasting by (1) using deep learning for improving the resolution of space-based satellite precipitation observations in areas where ground-radar data is lacking; (2) using the super-resolution results for estimating rain rates and...
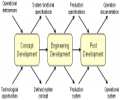
The Modeling & Simulation (M&S) project has four main tasks: (1) Understand how modeling and simulation is used in systems engineering in general, and in particular, at MSFC. We are interviewing key systems engineering practitioners and managers at MSFC, examining NASA systems...
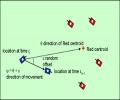
Sequences of events resulting from the actions of human adversarial actors such as military forces or criminal organizations may appear to have random dynamics in time and space. Finding patterns in such sequences and using those patterns in order to anticipate and respond to the events can be...
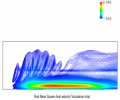
Direct numerical simulation (DNS) is being used to develop an erosive burning model of the booster. DNS resolves all relevant turbulent scales, and is capable of resolving several primary flames, such as the Ammonium perchlorate (AP) decomposition flame, and the decomposed AP and binder fuel...
Space weather, including the solar wind, produces physical phenomena, such as geomagnetic storms and ionospheric disturbances, that affect satellites in earth orbit and terrestrial communications systems. The U. S. Air Force Weather Agency (AFWA) uses computer models to predict space weather...
Historically, the propulsion system of a spacecraft can be 25-50% of the spacecraft wet mass (the spacecraft's mass before liftoff). Understanding the mass of the propulsion system early in the design process gives spacecraft mission planners a better understanding of the amount of mass that can...
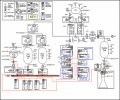
UAH's Spacecraft Propulsion Systems Engineering and Modeling project is focused on the support of the Reaction Control System (RCS) for NASA's Ares I launch vehicle. The developments of the pressurization system model and the overall propulsion system model are priorities for this project.
The Geostationary Operational Environmental Satellites (GOES) are in geosynchronous orbits that allow them to monitor a fixed spot on the Earth's surface. Data is transmitted and archived at fifteen minute intervals. This allows scientists to monitor and track weather conditions at up to 1 km...
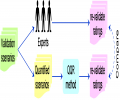
Increasingly, decisions are being made based partially or entirely on models. These decisions may be quite important, with the potential of serious or unacceptable consequences if an incorrect decision is made. The models used to support the decisions may have been newly developed or modified...
A simple question is how much stock one should hold on hand in anticipation of future need. Holding stock in inventory costs money, so a balance must be struck between the cost of inventory stock and the cost of unmet demand. The Inventory Analyst (IA) package has been successfully used and...
Beginning with an initial concept and model provided by the U. S. Army System Simulation and Development Directorate (SSDD), the University of Alabama in Huntsville (UAH) has developed and tested a “Metric of Evil,” a quantitative model of the harm associated with military courses of action...
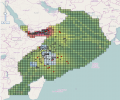
Due to Base Realignment and Closure (BRAC) actions, approximately 4,500 government positions and 15,000 contractor positions, concentrated in technical, logistical, and acquisition fields, will be moving to Huntsville Alabama over a five year period. Because of retirements, transfers, and job...
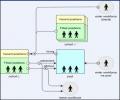
Probabilistic design analysis (PDA) is a methodology to assess component reliability for given failure modes in complex systems. PDA involves the modeling of the probability of integrated system failures which then can be used to focus design improvements for improved operational safety. UAH...
Unit-level combat models provide computational efficiency, with the result that they can simulate large scenarios in terms of geographic scope and size of military forces involved and are often able to execute much faster than real-time. However, existing unit-level combat models (such as...
The difficulty arises, of course, in selecting the two teams to play in the BCS Championship game. The BCS recognized that the media poll and the coaches' poll should be important components of the ranking system, but also recognized the emergence of computer rankings as reliable indicators of...
It is useful to have mathematical criteria for evaluating errors in map projections. The Chebyshev criterion for minimizing rms (root mean square) local scale factor errors for conformal maps has been useful in developing conformal map projections of continents. Any local error criterion will be...
The various primary systems of military aircraft and missiles (avionics, propulsion, sensors, and weapons) and the subsystems within them must exchange data in order to perform their functions. Integration testing for those systems and subsystems can be time-consuming, expensive, and difficult,...